毒物劇物取扱者.com

Advertisement

分子軌道のための指標表

当Website管理人は、化学のしろうとであり大学化学の専門書の持ち合わせもありません。

毒物劇物の試験問題で、水分子は折れ線であることをしり、最初はそうなんだ、とりあえずそう理解しておけば点数はとれるなと思っていました。

時間が経つと、素朴単純に、水素化ベリリウム　$\ce{BeH_2}$ は直線分子で、何で$\ce{H_{2}O}は、$折れ線なんだろうと思うようになり、Ytubeで特にインドや米国のオープン講座 Open Course Wareの動画とかを見渡しました。

Walsh diagramとかCharacter Table(指標表)とかでてきてまったくわかりませんでしたが、ちょこちょこ調べて、とりあえずわかる範囲で得たものを以下にまとめようと思いました。

毒物劇物の試験に関係ないものとなりましたが、そんなものもあるんだと見学していただければ幸いです。

物事を考えるときエネルギーや力の向きを土台にすべきですが、何せ素人ゆえに数式だけで精一杯になり化学的説明も欠如することもありご勘弁いただきたく存じます。また、化学の専門用語もわかりませんので英語のまま書くこともお許しください。

早速はじめましょう。

https://symotter.org/galleryに分子の軌道が見られるサイトがあります。

基本的には水分子に限定し、シンメトリーの様相についていくつかを例にとります。

分子を上から串刺しにした線を、principal axis といいその軸の回転操作を$ C_n $で表します。

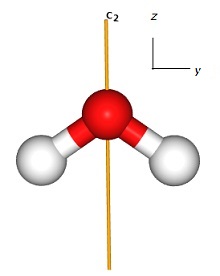
z軸上から見たとき酸素を中心に二つの水素があり、360°の1/2の回転操作を行うことができるので、水分子では$ C_2$と表します。

水分子を横から見たもので、z軸に垂直（vertical）なy軸との平面を設定します。

この面は反射像を描き、対象であれば1、非対称であれば-1とします。

一般には$ \sigma_{v}^{'}(yz)$としるします。

「$'$」の点は、プライム　prime と呼びます。

数学的には素数的な意味のようですが特に気にしないようにしています。

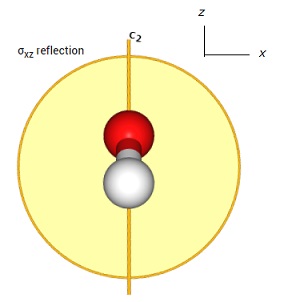
水分子を真正面から見た場合、z軸と直角なy軸の面を設定します。

この面は反射像を描き、対象であれば1、非対称であれば-1とします。

一般には$ \sigma_{v}(yz)$としるします。

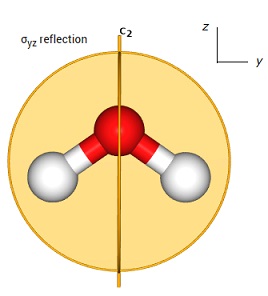
水分子には、$ C_2$、$ \sigma_{v}^{'}(yz)$、$ \sigma_{v}(xz)$の三つの対称操作が存在します。

三つの操作を描いたものが下の図です。

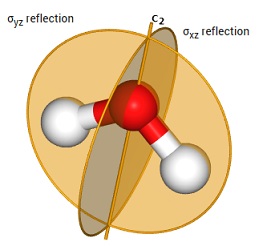
対称操作には、このほかに invers があります。

$\ce{C_{2}H_{2}Br_{2}Cl_{2}}$（1,2-ジブロモ-1,2-ジクロロエタン）は、下の図のように中心座標に対して、x y z をすべて反転します。

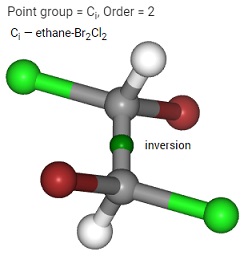
$ \sigma$は、$v,h,d$の三種類があります。

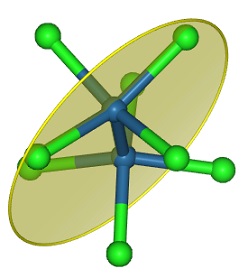
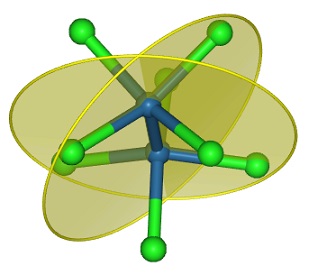
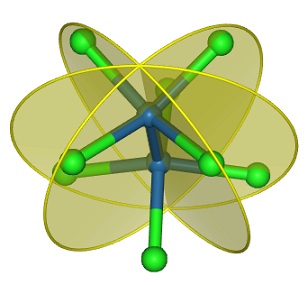
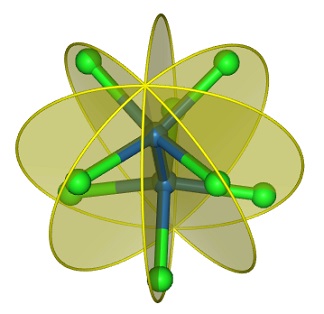
phosphorous pentafluorid 五弗化燐ではprincipal axis $C_3$と直角な水平（Horizontal）な面を$ \sigma _h$で表します。

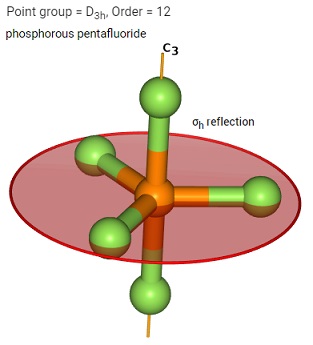
improper rotation は　$ S_n$であらわされますが、$ S_{n}=C_{n} \cdot \sigma _h$と等価です。

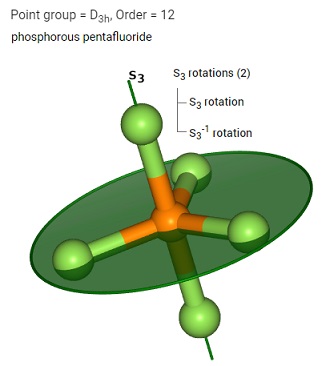
$\ce{ [Os{2}Cl{8}]^{2-}}$は $ \sigma _d$をもち、これは$ \sigma _v$の変型判で2軸の中間や分割された面での反射（Diagonal or dihedral reflection ）です。

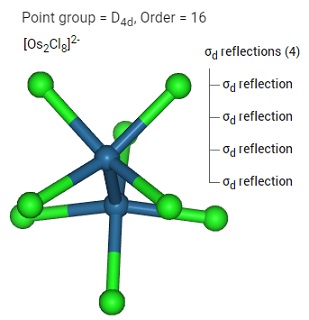
水分子の指標表 character tableです。

$$ $$ \( \begin{array}{c|cccc} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline A_1 & 1 & 1 & 1 & 1 \\ A_2 & 1 & 1 & -1 & -1 \\ B_1 & 1 & -1 & 1 & -1 \\ B_2 & 1 & -1 & -1 & 1 \end{array} \) $$ $$

$ C_2 $、$ \sigma_{v}(xz)$、 $ \sigma_{v}^{'}(yz) $ は、上で示しましたが$ E$は、identity とよばれる恒等操作です。

そのままという数字でいえば1、あるいは1倍で、数学的には（群論で）なくてはならない元です。

行列を用いるとx、y、z座標では次のように表せます。

\( x \rightarrow x \\ y \rightarrow y \\ z \rightarrow z \\ E : \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$

行列の対角線をトレースしたものがcharacterとよばれ次のように表します。

$ trace(E)= \chi (E)=1+1+1=3$

となります。

$$ $$

characteristic　は指標と訳されています。

$E$のように3次元の行列が1次元のただの数値になってしまったものがcharacterです。

複雑な行列を一言で数値で表したようなものになります。

ここからcharacter tableの成り立ちや分子との関係を考えます。

$2p_x$軌道に$C_2$操作を施すことを考えます。

$2p_x$軌道を対称対象、$C_2$が対称操作と呼んだりします。

$2p_x$軌道に$ C_2 $操作をおこなうと次のように式で表せます。

\( C_2 \cdot 2p_x=(-1)2p_x \) $$ $$

$z$軸周りに$C_2$操作を行うことは、電子雲のプラスマイナスが入れ替わりますから、非対称であることを$-1$で表しています。

実際は$2p_x$軌道を回転できませんから、$z$の回転に対して、非対称の位置情報になっていることを$-1$が示していることになります。

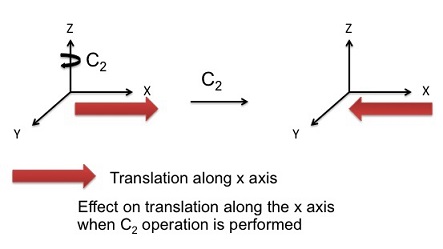
$C_2$操作は、$z$軸をそのままの状態で$x$軸、$y$軸のデータを反転することを意味します。

これを行列を用いて表します。

\( x \rightarrow -x \\ y \rightarrow -y \\ z \rightarrow z \\ C_2 : \begin{pmatrix} \cos \pi & \sin \pi &0 \\ -\sin \pi & \cos \pi &0 \\ 0 &0 &1 \\ \end{pmatrix} = \begin{pmatrix} -1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$

ちなみに$C_2$の指標は

$ \chi (E)=-1-1+1=-1$

となります。

$$ $$

反射reflectionを考えます。

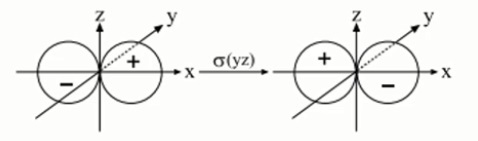
$ \sigma _{v}^{'}(yz) \cdot p_{x} =(-1)p_x$

となります。

引用する図によってx、y、z座標が変わりますのでご勘弁ください。

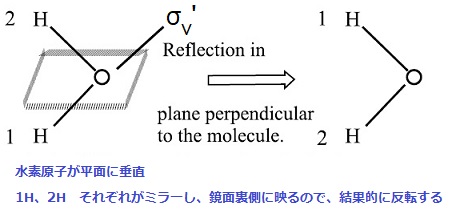
面手前の水素が、面にめり込んで$x$軸のマイナスの位置にあるのが反射した水素です。

$ \sigma _{v}^{'}(yz) $面に対して相対して存在する水素は別物ですので、水素は非対称です。

非対称ということで$x$座標だけ$-1$で表せます。

ただし、$y$軸では、対称のまま変化がありませんので$ \sigma _{v}(yz) \cdot p_{y} =(1)p_y$となります。

\( x \rightarrow -x \\ y \rightarrow y \\ z \rightarrow z \\ \sigma _{v}^{'}(yz) : \begin{pmatrix} -1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$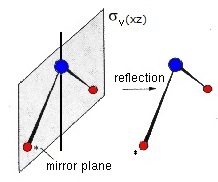

$ \sigma _{v}(xz) \cdot p_{x} =(1)p_x$

鏡に水分子の全体が映ります。

水分子のすべての原子を含む面が$ \sigma _{v}(xz)$です。

水分子は、鏡にたいしてそのままです。

反射操作の機能を持っていない、$x$軸でそのままということで$1$で表せます。

水分子が$ \sigma _{v}(xz)$面に張り付いていれば、鏡に映ればそのまま映ります

ただし、$y$軸では、$ \sigma _{v}(xz) \cdot p_{y} =(-1)p_y$となります。

\( x \rightarrow x \\ y \rightarrow -y \\ z \rightarrow z \\ \sigma _{v}(xz) : \begin{pmatrix} 1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$

$x$軸に対する対称操作を考えます。

$E$はそのままですから$(1)p_x$。

$C_{2}$は回転し変化しますので$(-1)p_x$。

$ \sigma_{v}(xz)$平面では$x$が面にピッタリ張り付いていますのでそのままです。$(1)p_x$。

$ \sigma_{v}^{'}(yz)$平面では、$x$軸は面を突き抜けて面の反対側に存在し得るが、その軌道は鏡の前の軌道を異なりますので非対称になりますので$(-1)p_x$。

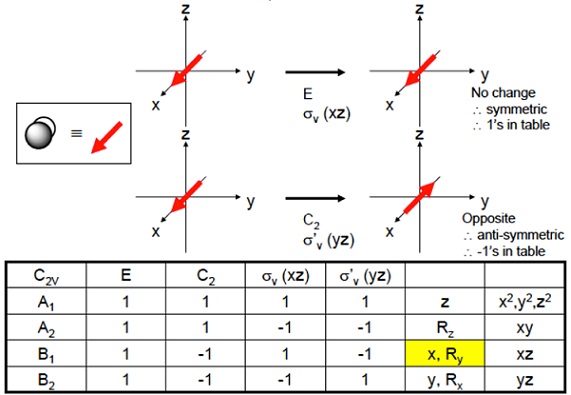
$x$軸に対する対称操作の結果をまとめたものを$B_1$とおきます。

$$ $$ \( \begin{array}{c|cccc|c} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline B_1 & 1 & -1 & 1 & -1 & x \\ \end{array} \) $$ $$

$z$軸に対する対称操作を考えます。

$E$はそのままですから$(1)p_z$。

$C_{2}$は回転し変化してもそのままですので$(1)p_z$。

$ \sigma_{v}(xz)$平面では$z$が面にピッタリ張り付いていますのでそのままです。$(1)p_z$。

$ \sigma_{v}^{'}(yz)$平面では、$z$軸にピッタリ張り付いていますのでそのままです。$(1)p_x$。

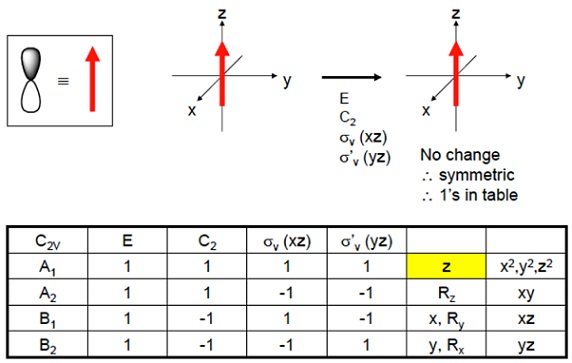
$z$軸に対する対称操作の結果をまとめたものを$A_1$とおきます。

$$ $$ \( \begin{array}{c|cccc|c} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline A_1 & 1 & 1 & 1 & 1 & z \\ \end{array} \) $$ $$

水分子で対称操作をした図も示しておきます。

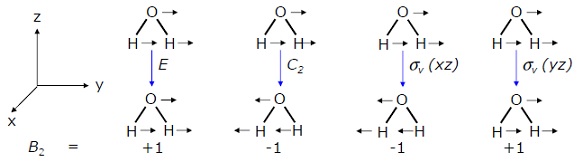
$p_{y}$軌道に対する対称操作の結果をまとめたものを$B_2$とおきます。

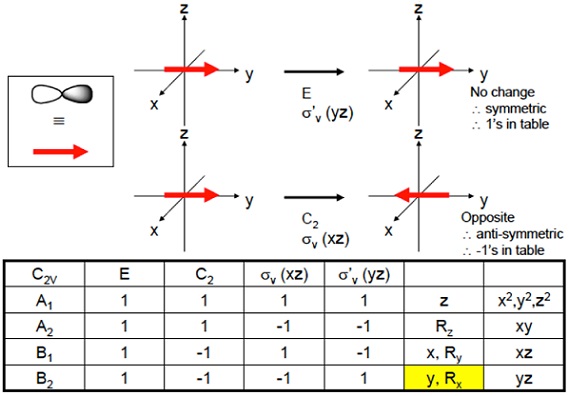
$E \cdot p_{y}=(1)p_{y}$　標記 $1$

$C_2 \cdot p_{y}=(-1)p_{y}$　標記 $-1$

$ \sigma_{v}(xz) \cdot p_{y}=(-1)p_{xy}$　標記 $-1$

$ \sigma_{v}^{'}(yz) \cdot p_{y}=(1)p_{y}$　標記 $1$

$$ $$ \( \begin{array}{c|cccc|c} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline B_2 & 1 & -1 & -1 & 1 & y \\ \end{array} \) $$ $$

水分子で対称操作をした図も示しておきます。

$\ce{_{8}O}$の電子軌道は、

$\ce{_{8}O}$ 1s ↑↓ 2s↑↓ 2p_x↑↓ 2p_y↑↓ 2p_z↑↓

ですが、ここだけ$d$軌道を考えさせてください。

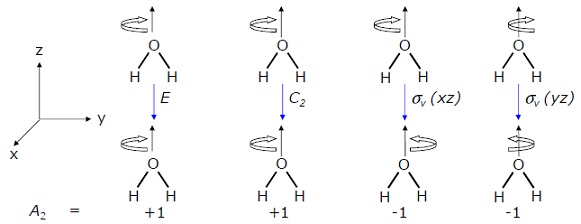
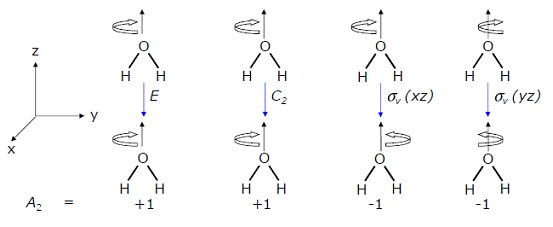
$3d_{xy}$軌道に対する対称操作の結果をまとめたものを$A_2$とおきます。

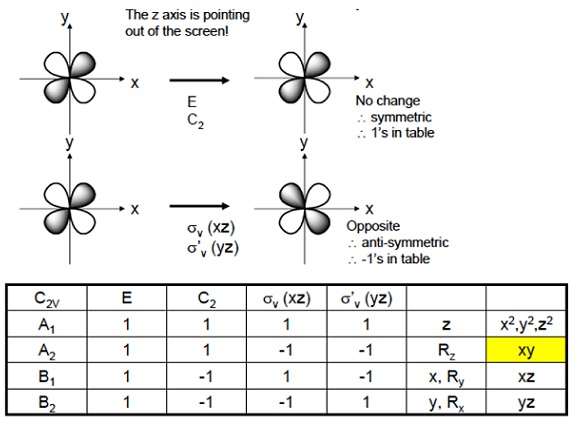
$E \cdot d_{xy}=(1)d_{xy}$　標記 $1$

$C_2 \cdot d_{xy}=(1)d_{xy}$　標記 $1$

$ \sigma_{v}(xz) \cdot d_{xy}=(-1)d_{xy}$　標記 $-1$

$ \sigma_{v}^{'}(yz) \cdot d_{xy}=(-1)d_{xy}$　標記 $-1$

\( \begin{array}{c|cccc|c} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline A_2 & 1 & 1 & -1 & -1 & xy \\ \end{array} \) $$ $$

少しきれいな画像も載せておきます。

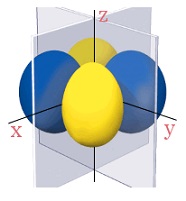
回転しても変わりませんが、2つの鏡に対しては変化がありますから$-1$となることが分かります。

\( x \rightarrow -x \\ y \rightarrow -y \\ z \rightarrow z \\ \begin{pmatrix} -1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$

これらをまとめますと次のようにcharacter tableになります。

$$ $$ \( \begin{array}{c|cccc|c} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) & \small{2p 軌道 ,3d 軌道} \\ \hline A_1 & 1 & 1 & 1 & 1 & z \\ A_2 & 1 & 1 & -1 & -1 & xy\\ B_1 & 1 & -1 & 1 & -1 & x \\ B_2 & 1 & -1 & -1 & 1 & y \end{array} \) $$ $$

character table の特徴

各要素の数値を文字に置き換えました。

$$ $$ \( \begin{array}{c|cccc} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline \varGamma _1 & k_1 & k_2 & k_3 & k_4 \\ \varGamma _2 & l_1 & l_2 & l_3 & l_4 \\ \varGamma _3 & m_1 & m_2 & m_3 & m_4 \\ \varGamma _4 & n_1 & n_2 & n_3 & n_4 \end{array} \) $$ $$

対称操作のまとめを行・行列$R$にしておきます。

$R=( E \quad C_2 \quad \sigma_{v}(xz) \quad \sigma_{v}^{'}(yz))$

$C_2v$　pint group のclass $h$ は対称操作が4つあるので4です。

$ h=4$です。

既約表現$ \varGamma_n$の各二乗の合計はclassに等しくなるルールがあります。

$k_1 ^{2}+ k_2^{2}+ k_3^{2}+ k_4^{2}=1^{2}+1^{2}+1^{2}+1^{2}=4$

$l_1 ^{2}+ l_2^{2}+ l_3^{2}+ l_4^{2}=1^{2}+1^{2}+(-1)^{2}+(-1)^{2}=4$

‥

既約表現とは、行列をこれ以上簡略化できないものをいいます。

まだ、簡略化できるものは可約表現といいます。

$ \displaystyle \sum_{i=1}^{class} [\chi_{i} (R)]^{2}=h $

ちなみに

$ \chi_{1}(E)=k_1=1$、$ \chi_{2}(C_2)=k_2=1$、$ \chi_{3}(\sigma_{v}(xy))=k_3=1$　‥です。

縦のデータでも同じルールが成り立ちます。

$k_1^{2}+l_2^{2}+m_1^{2}+n_1^{2}=1^{2}+1^{2}+1^{2}+1^{2}=4$

‥

$ \displaystyle \sum_{i=1}^{class} \chi_{i}(R)\cdot \chi_{j} (R)=0 \quad i \neq j $

$\varGamma _1$と $\varGamma _2$の掛け算は、直角構造、直交しているので$0$になるというルールです。

$1\cdot(1)+ 1\cdot(1)+ 1\cdot(-1)+ 1\cdot(-1) \\ \quad =1+1-1-1=0$

既約表現同士の加算も可能です。

$$ $$ \( \begin{array}{l|cccc} A_1 & 1 & 1 & 1 & 1 \\ A_1 & 1 & 1 & 1 & 1 \\ A_2 & 1 & 1 & -1 & -1 \\ \hline 2A_{1}+A_{2} & 3 & 3 & 1 & 1 \end{array} \) $$ $$

上の式を$ \varGamma =2A_{1}+A_{2}=(3 \quad 3 \quad 1 \quad 1)$と表しましょう。

$2A_{1}+A_{2}$の係数、2、1をReduction formulaから求めてみましょう。

$$ $$ $ \displaystyle a_{i}= \frac{1}{h}\sum_{R}^{class} \chi(R)\cdot \chi_{i} (R)\\ h:order \quad C_{2v}=4 \\ a_{i}:\small{既約表現の係数}\\ \chi (R):\chi \small{の指標}\\ \chi_{i}(R):\chi_i \small{の指標}\\ A_{1}=(1\quad 1 \quad 1 \quad 1)\\ a_{1}=\frac{1}{h}(3\cdot 1 \cdot 1+3 \cdot 1 \cdot 1+ 1 \cdot 1 \cdot 1+ 1 \cdot 1 \cdot 1)\\ \quad =\frac{8}{4}=2 $ $$ $$

最初の3は、$\varGamma$の3、次の1は$A_1$指標の$E$の数値、そして対称操作$E$の係数の1を掛けたものが最初の$ 3 \cdot 1 \cdot 1$となっており、以下同様の順序で計算していきます。

\( a_{2}=1\\ b_{1}=0\\ b_{2}=0\) $$ $$

上の$ a_{1}=2 \quad a_{2}=1$が$ \varGamma =2A_{1}+A_{2}$の係数に対応していることが分かります。

ここで指標表をもう少し考えます。

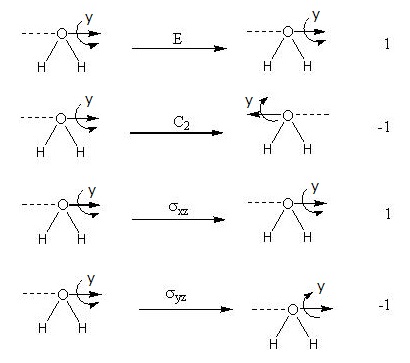
Rotation という回転操作そのものを対象として対称操作をまとめてみます。

$R_z$周りの$E$と$C_2$は、軸に張り付いていて変化なくそのままです。

回転方向が、図によっては時計回り、あるいは反時計回りになっていますが統一的に扱えばどちら周りでもかまいません。

ちなみに数学屋さんにおいては、反時計回りを正回転としています。

ふたつの$ \sigma$操作はいずれも反射鏡に対して反対回りしますので非対称、矢印が逆という変化があるので$(-1)$になります。

まとめると図のようになります。

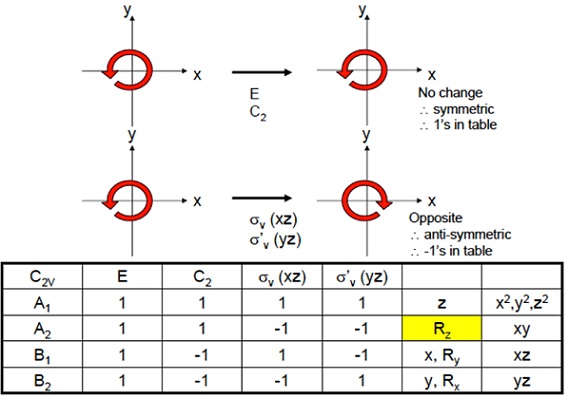
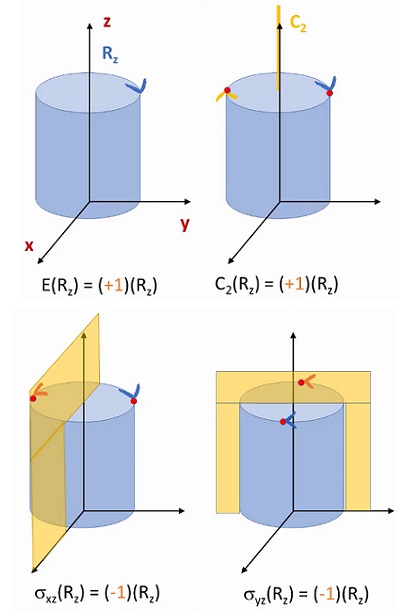
矢印に着目します。

$R_x$の$E$は、そのままです。

$R_x$の$C_2$操作は、回転すると矢印が逆になるので非対称で$(-1)$となります。

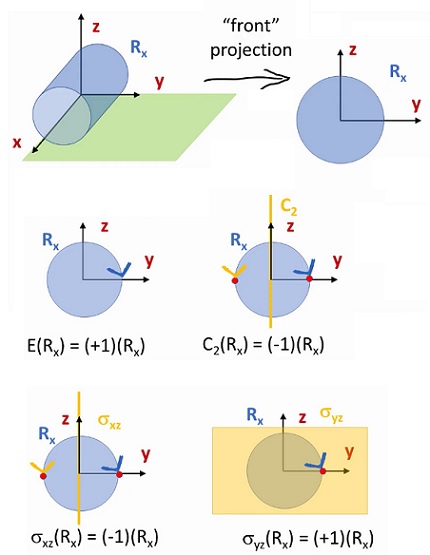
$R_x$の$ \sigma _{xz}$は、$y$軸で面にめり込むと矢印は変わりますので非対称ということになります。

ここは分かりにくく海外のサイトも間違って説明しているものも多く、図に示します。

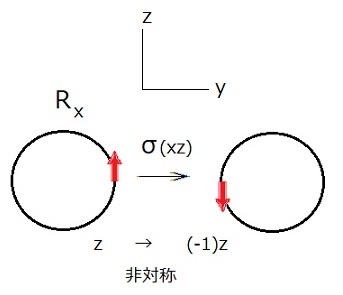
式で書いてみましょう。

$$ $$ \( R_{x}: \begin{pmatrix} 1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &-1 \\ \end{pmatrix} \) $$ $$ \( \sigma_{xz}: \begin{pmatrix} 1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$ \( \begin{pmatrix} 1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &-1 \\ \end{pmatrix} \begin{pmatrix} 1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &1 \\ \end{pmatrix} = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &-1 \\ \end{pmatrix} \) $$ $$ \( x \rightarrow x \\ y \rightarrow y \\ z \rightarrow -z \) $$ $$

間違う理由は、$ \sigma_{xz} \cdot x =(+1)x$と$\sigma_{xz} \cdot R_{x} =(-1)R_x$の違いです。

$x$は$x$軸の並進 transform で、$R_x$は$x$軸周りの回転 rotationです。

向きが回転していて、さらに$x$を基準に回りますから実際に向きの状態は$z$軸です。

この$z$の鏡面$ \sigma_{xz}$を考えますのですこし混乱しましたね。

回転は持続的に動いていますので、ここでは矢印の向きの判断がわかりやすいので180°として扱っています。

行列で$R_x$をかけば$x$が基準で$yz$平面を180°回転させますので$y→-y$、$z→-z$となりますから以下の通りです。

\( R_x : \begin{pmatrix} 1 &0 &0 \\ 0 &-1 &0 \\ 0 &0 &-1 \\ \end{pmatrix} \) $$ $$

$R_x$の指標は

$ \chi (R_x)=1-1-1=-1$

となります。

$R_x$の$ \sigma (yz)$は、$x$軸で面にめり込んでも矢印が変わりませんので対称ということになります。

$R_y$について考えます。

$R_y$の$E$は、そのままです。

$R_y$の$C_2$操作は、回転すると矢印が逆になるので非対称で$(-1)$となります。

$R_y$の$ \sigma _{xz}$は、$y$軸で面にめり込むと矢印が変わりませんので対称ということになります。

$R_y$の$ \sigma _{yz}$は、$x$軸で面にめり込むと矢印は変わりますので非対称ということになります。

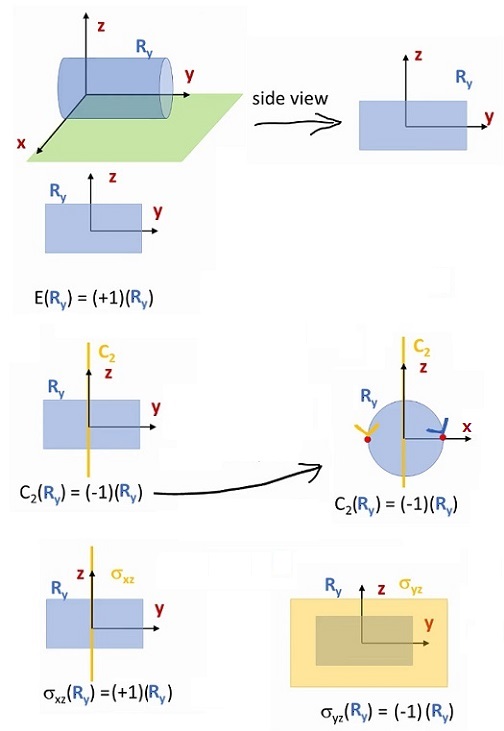
全部は説明できませんでしたが、指標表を示します。

$$ $$ \( \begin{array}{c|cccc|l} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) & \ \\ \hline A_1 & 1 & 1 & 1 & 1 & z,x^{2},y^{2},z^{2} \\ A_2 & 1 & 1 & -1 & -1 & R_{z},xy \\ B_1 & 1 & -1 & 1 & -1 & x,R_{y},xz \\ B_2 & 1 & -1 & -1 & 1 & y,R_{x},yz \\ \hline \end{array} \) $$ $$

水分子のノーマル・モデル

水分子の基本形を考えます。

$$ $$ \( E:\\ x_1 \rightarrow x_1 \\ y_1 \rightarrow y_1 \\ z_1 \rightarrow z_1 \\ x_2 \rightarrow x_2 \\ y_2 \rightarrow y_2 \\ z_2 \rightarrow z_2 \\ x_3 \rightarrow x_3 \\ y_3 \rightarrow y_3 \\ z_3 \rightarrow z_3 \\ \) $$ $$ \( E: \\ \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \\ x_2 \\ y_2 \\ z_2 \\ x_3 \\ y_3 \\ z_3 \\ \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \\ x_2 \\ y_2 \\ z_2 \\ x_3 \\ y_3 \\ z_3 \\ \end{pmatrix} \) $$ $$ \( \chi (E)=1+1+1+1+1+1+1+1+1=9 \\ \) $$ $$ \( C_{2}:\\ x_1 \rightarrow -x_1 \\ y_1 \rightarrow -y_1 \\ z_1 \rightarrow z_1 \\ x_2 \rightarrow -x_3 \\ y_2 \rightarrow -y_3 \\ z_2 \rightarrow z_3 \\ x_3 \rightarrow -x_2 \\ y_3 \rightarrow -y_2 \\ z_3 \rightarrow z_2 \\ \) $$ $$

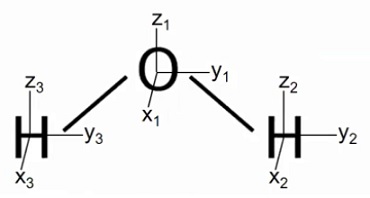
回転で$x_{2},y_{2},z_{2}$系　と$x_{3},y_{3},z_{3}$系　が入れ替わります。

\( C_{2}: \\ \left( \begin{array}{ccc|ccc|ccc} -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \hline 01 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} \right) \begin{pmatrix} x_1 \\ y_1 \\ z_1 \\ x_2 \\ y_2 \\ z_2 \\ x_3 \\ y_3 \\ z_3 \\ \end{pmatrix} = \begin{pmatrix} -x_1 \\ -y_1 \\ z_1 \\ -x_3 \\ -y_3 \\ z_3 \\ -x_2 \\ -y_2 \\ z_2 \\ \end{pmatrix} \) $$ $$ \( \chi (C_{2})=-1-1+1=-1 \\ \)

反射$\sigma(xz)^{'}$でも$x_{2},y_{2},z_{2}$系　と$x_{3},y_{3},z_{3}$系　が入れ替わります。

$$ $$ \( \sigma(xz)^{'}: \\ \left( \begin{array}{ccc|ccc|ccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \hline 01 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} \right) \begin{pmatrix} x_1 \\ y_1 \\ z_1 \\ x_2 \\ y_2 \\ z_2 \\ x_3 \\ y_3 \\ z_3 \\ \end{pmatrix} = \begin{pmatrix} x_1 \\ -y_1 \\ z_1 \\ x_3 \\ -y_3 \\ z_3 \\ x_2 \\ -y_2 \\ z_2 \\ \end{pmatrix} \) $$ $$ \( \chi (\sigma(xz)^{'})=1-1+1=1 \\ \) $$ $$ \( \sigma(yz)^{'}: \\ \left( \begin{array}{ccc|ccc|ccc} -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \hline 01 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right) \begin{pmatrix} x_1 \\ y_1 \\ z_1 \\ x_2 \\ y_2 \\ z_2 \\ x_3 \\ y_3 \\ z_3 \\ \end{pmatrix} = \begin{pmatrix} -x_1 \\ y_1 \\ z_1 \\ -x_2 \\ y_2 \\ z_2 \\ -x_3 \\ y_3 \\ z_3 \\ \end{pmatrix} \) $$ $$ \( \chi (\sigma(yz)^{'})=-1+1+1-1+1+1-1+1+1=3 \\ \) $$ $$

水分子のノーマル形は次の既約表現となります。

\( \Gamma_{nuclear}=[9 \hspace{13pt}-1 \hspace{13pt} 1 \hspace{13pt} 3]\) $$ $$

$x,y,z$の各軸の変換transform(並進)を求めます。

\( E:\\ x \rightarrow x \\ y \rightarrow y \\ z \rightarrow z \\ \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$ \( \chi (E) =1+1+1=3 \\ \) $$ $$ \( C_{2}:\\ x \rightarrow -x \\ y \rightarrow -y \\ z \rightarrow z \\ \begin{pmatrix} -1 &0 &0 \\ 0 & -1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$ \( \chi (C_{2}) =-1-1+1=-1 \\ \) $$ $$ \( \sigma(xz)_{'}:\\ x \rightarrow x \\ y \rightarrow -y \\ z \rightarrow z \\ \begin{pmatrix} 1 &0 &0 \\ 0 & -1 &0 \\ 0 &0 &1 \\ \end{pmatrix} \) $$ $$ \( \chi (\sigma(xz)_{'}) =1-1+1=1 \\ \) $$ $$ \( \sigma(yz)_{'}:\\ x \rightarrow -x \\ y \rightarrow y \\ z \rightarrow z \\ \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \) $$ $$ \( \chi (\sigma(yz)_{'}) =-1+1+1=1 \\ \) $$ $$

水分子の変換は次の既約表現となります。

\( \Gamma_{x,y,z}=[3 \hspace{13pt}-1 \hspace{13pt} 1 \hspace{13pt} 1]\)

実はcharacter tableで、$x$は、B₁に$y$はB₂に$z$は、A₁に含まれますので、A₁+B₁+B₂の合計が\( \Gamma_{x,y,z}\)と同じ結果になります。

次に定常状態、unshifted atomの既約表現を求めてみます。

$$ $$ \( E: \\ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} H_{a} \\ H_{b} \\ O \\ \end{pmatrix} \) $$ $$ \( \chi (E ) =1+1+1=3 \\ \) $$ $$ \( C_{2}: \\ \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} H_{a} \\ H_{b} \\ O \\ \end{pmatrix} \) $$ $$ \( \chi (C_{2} ) =0+0+1=1 \\ \) $$ $$ \( \sigma (xz)^{'}: \\ \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} H_{a} \\ H_{b} \\ O \\ \end{pmatrix} \) $$ $$ \( \chi (\sigma(xz)^{'}) =0+0+1=1 \\ \) $$ $$ \( \chi (C_{2} ) =0+0+1=1 \\ \) $$ $$ \( \sigma (yz)^{'}: \\ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} H_{a} \\ H_{b} \\ O \\ \end{pmatrix} \) $$ $$ \( \chi (\sigma(yz)^{'}) =1+1+1=3 \\ \) $$ $$

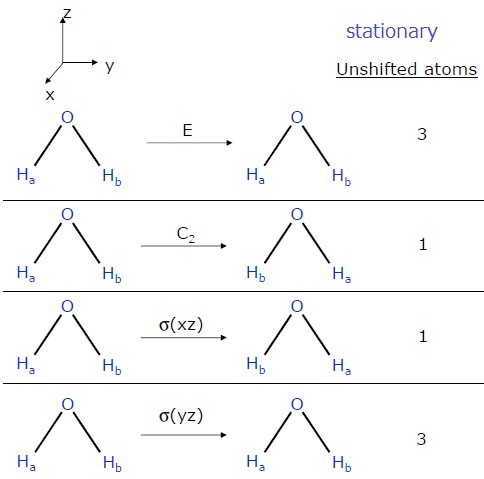
\( \Gamma_{stationary}=[3 \hspace{13pt}1 \hspace{13pt} 1 \hspace{13pt} 3]\)

となります。

実は、$\Gamma_{stationary}$に$\Gamma_{x,y,z}$をかけたものが$\Gamma_{nuclear}$になっています。

この関係を満たすものが$\Gamma_{stationary}$ということになります。

\( \begin{array}{l|cccc} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline \Gamma _{x,y,z} & 3 & -1 & 1 & 1 \\ \hline \Gamma _{stationary} & & & & \\ \hline \Gamma _{nuclear} & 9 & -1 & 1 & 3 \\ \end{array} \) $$ $$

$\Gamma_{nuclear} =\Gamma_{stationary} \cdot \Gamma_{x,y,z}$

\( \begin{array}{l|cccc} C_{2v} & E & C_2 & \sigma_{v}(xz) & \sigma_{v}^{'}(yz) \\ \hline \Gamma _{x,y,z} & 3 & -1 & 1 & 1 \\ \hline \Gamma _{stationary} & {\color{red} 3} & {\color{red}1 } & {\color{red}1 } & {\color{red} 3} \\ \hline \Gamma _{nuclear} & 9 & -1 & 1 & 3 \\ \end{array} \) $$ $$

ここで一旦、データをまとめます。

ノーマルモードと称した分子軌道全体の既約表現を以下とします

$\Gamma_{reducible}=[9 \hspace{13pt}-1 \hspace{13pt} 1 \hspace{13pt} 3 ] $

$ \Gamma _{x,y,z}$と称した並進を以下の既約表現とします。

$\Gamma_{translational}=[3 \hspace{13pt}-1 \hspace{13pt} 1 \hspace{13pt} 1 ] $

回転をの既約表現を以下とします。

$\Gamma_{rotational}=[3 \hspace{13pt}-1 \hspace{13pt} -1 \hspace{13pt} -1 ] $

そして最後にstationaryとかunshiftedと称したものを振動しして既約表現を以下とします。

$\Gamma_{vibrational}=[3 \hspace{13pt}1 \hspace{13pt} 1 \hspace{13pt} 3 ]$

これらには次の関係があります。

$\Gamma_{reducible}=$

$\Gamma_{vibrational}+\Gamma_{rotational} + \Gamma_{translational}$

$\Gamma_{reducible}$を求めておけば、水分子全体の並進、回転、振動を表現することができます。

$\Gamma_{reducible}$の係数の求め方は上で述べた$a_i$と同じやり方なので省略します。

$\Gamma_{reducible}=3A_{1}+A_{2}+2B_{1}+3B_{2}$

となります。

説明が長くなりましたので次のページに移りたいと思います。

Advertisement